Классы эквивалентности номер дома

В данном примере важно помнить что подобное применение классов эквивалентности возможно только в случае если есть полная уверенность в том что за обработку удалений отвечает один и тот же код. В любом случае возможность познать систему чуть глубже окажет позитивный эффект на тестирование.

Если же у вас достаточно времени на проведение 20ти тестов, то следует провести эти 20 тестов и спать спокойно. Жаль что времени почти всегда не хватает.

Граничные значения

В отличии от классов эквивалентности техника тест дизайна гордо именуемая Граничные значения произошла не из наблюдения за однотипным поведением тестируемых систем, а из часто наблюдаемых багов в определенных ситуациях. Довольно часто именно на границах диапазонов допустимых значений появляются довольно неприятные баги. Причин у этого может быть много но нас как тестировщиков не интересует что вызывает эти баги, нерадивость программиста или баг в фреймворке который он использует или возможно наш знак зодиака, нам важно знать в каких условиях возник баг.

Граничные значения являются идейным продолжением классов эквивалентности так как именно на границах этих классов проявляются, так интересующие нас, граничные значения.

Граничными значениями как видно являются 1 и 1000. Поскольку эта техника подразумевает проверку не только граничного значения но и двух соседних то к нашему набору тестов прибавятся еще 6 проверок (0, 1, 2, 999, 1000, 1001).

Сами диапазон допустимых значений и особенно их границы за частую не так тривиальны как в нашем примере, но если вы можете их выделить и скомбинировать с классами эквивалентности то вы получите хорошее (качественное) покрытие тестами вашей функциональности.

Эпилог

Классы эквивалентности и граничные значения одни из базовых техник тест дизайна, но несмотря на кажущуюся простоту и примитивность этих техник они очень полезны и могут в несколько раз сократить время необходимое на один тест раунд. А как показывает практика именно этот ресурс самый ценный в нашей жизни и работе и что особенно не честно невосполнимый.

Источник

говориМ о тестировании
простым языком

Тест-дизайн. Классы эквивалентности и граничные значения

В этой статье мы разберем одну из самых известных и фундаментальных техник, технику выделения классов эквивалентности и граничных значений.

В чем суть техники?

Основная задача определения классов эквивалентности и граничных значений — «уйти» от дублирующих проверок. Таким образом, мы сократим количество однотипных тестов до необходимого минимума. Как это можно представить?

Предположим, у нас много-много разных булок, сделаны они по одному рецепту, а вот форма у них немного разная. А теперь представьте, что вам необходимо определить вкус каждой булки. Что вы будете делать? Попробуете все или возьмете только одну, потому что остальные сделаны аналогично? Я думаю второй вариант будет более оптимальным)

В тестировании ситуация аналогичная. Только вместо булок наши тесты. И все немного сложнее.

Классы эквивалентности

Сначала дадим определение классам эквивалентности.

Эквивалентная область (equivalence partition) —часть области входных или выходных данных, для которой поведение компонента или системы, основываясь на спецификации, считается одинаковым.

Скорей всего было не очень понятно…

Проще говоря, любой тест, выполненный из одного и того же класса эквивалентности, приведет к точно такому же результату, как и выполнение всех остальные тестов из этого же класса.

Например, у нас есть 10 тестов из одного класса. Если один из этих тестов проходит корректно, и то все остальные пройдут корректно. И наоборот, если один из тестов приведет к падению системы, то и все остальные тесты, также приведут к падению.

Пока все еще абстрактно, давайте конкретизируем. Предположим, у нас планируется акция «Скидка 10% на покупку от 5 товаров». Нам необходимо проверить функционал скидки в зависимости от количества товаров. Что будем делать? Есть два варианта проверки:

Тестов получается очень много.

2. Попробовать выделить классы эквивалентности и оптимизировать проверки.

Пойдем по второму варианту, он более эффективный. У нас всего два разных результата выполнения теста – со скидкой и без скидки. Логично предположить, что класса эквивалентности тоже будет два. В одном тесты будут проверять наличие скидки в 10%, в другом ее отсутствие.

Графически это можно представить следующим образом:

Т.е. какой бы мы тест не взяли из первого класса, мы получим скидку в 0%, аналогично для второго класса эквивалентности.

Теперь теория и здравый смысл подсказывают нам, что можно взять не все тесты, а только несколько из каждого класса эквивалентности. Этого должно быть достаточно, чтобы проверить оба случая со скидкой.

Но теперь вопрос, какие тесты брать? Есть ли разница между ними, может быть все-таки есть небольшие отличия?

Граничные значения

Путем долгого времени наблюдения за разработкой и анализа багов, специалисты пришли к выводу, что большинство ошибок возникает именно на границах между классами эквивалентности. Т.е. нам в первую очередь важно проверить переходы на стыке границ каждого класса, так как именно там велик риск возникновения ошибок.

Поэтому для эффективного тестирования нам необходимо выделить у каждого класса граничные значения. Давайте попробуем сделать на нашем примере:

Итого, 4 теста вместо 100 с учетом сохранения тестового покрытия.

Наша задача, как тестировщика, уметь правильно определить и работать с классами эквивалентности и граничными значениями. Выше мы рассмотрели пример с позиции черного ящика. У него есть существенные минус, мы не знаем как реализована работа функционала с точки зрения кода. Следовательно, не можем со 100% уверенностью правильно выделить классы эквивалентности.

Давайте рассмотрим пример посложней. Нам необходимо проверить корректность бокового меню на сайте из 10 страниц. Вот такое:

Страницы сами по себе одинаковые и отличаются только содержанием, боковое меню зрительно полностью идентично.

Только что пройденный материал подсказывает нам, что есть один класс эквивалентности и он включает в себя все 10 страниц. Но на практике есть как минимум два варианта:
1. Если сайт сделан на HTML, в том числе и боковое меню, то необходимо проверять КАЖДУЮ страницу, так как на каждой странице боковое меню работает отдельно от остальных.
2. Если сайт сделан с помощью, например, шаблонизаторов, то тогда выделить 10 страниц в класс эквивалентности можно, так как код меню хранится отдельно.

Т.е. в зависимости от реализации, классы будут разные. Как это определить? Если вы знаете языки программирования и у вас есть доступ в репозиторий, то посмотреть в код. Если вы не поняли, что я сейчас написал, то подойдет и второй вариант) Поговорите с программистом, который делал эту функциональность и уточните у него, правильно ли вы делаете.

Источник

Тестовые примеры. Классы эквивалентности. Ручное тестирование в MVSTE

5.2.2 Классы эквивалентности

Рассмотрим другой пример.

Функция, которую будем тестировать:

После исправлений функциональное требование 4.2.1.1. будет выглядеть так:

Тестирование на допустимые данные ничем не будет отличаться от тестирования функции деления. Составим классы эквивалентности.

Учитывая то, что у нас два идентичных входных параметра, для полного рассмотрения всех классов эквивалентности необходимо составить и проверить 7*7=49 тестовых примеров, что все равно гораздо меньше, чем полный перебор.

При этом, как показал тест с делением, ошибка может проявиться лишь в нескольких из этих примеров, которые не сильно отличаются от остальных граничных классов эквивалентности.

Некоторые классы эквивалентности не удовлетворяют требованию 4.2.1.1. так как выводят сумму за допустимые пределы. Поведение метода на таких входных данных описано в требовании 4.2.1.2.

На рис.5.2 показано возможное выделение классов эквивалентности (цветами изображены области корректных и некорректных значений, а кружками — сами классы эквивалентности):

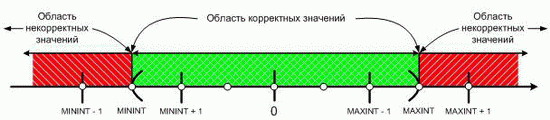
Иногда удобнее составить классы эквивалентности по выходному параметру (в данном случае их будет 7) и уже по ним подбирать входные данные и составлять тестовые примеры.

Основной способ поиска дефектов – передача системе данных, не предусмотренных требованиями: слишком длинных или слишком коротких строк, неверных символов, чисел за пределами вычислимого диапазона и т.п. Неверные данные, как и допустимые, также можно разделять на различные классы эквивалентности. В качестве простого примера снова рассмотрим функцию сложения.

Замечание. Как уже отмечалось выше, тест-требования составлены очень подробно и, фактически, соответствуют тестовым примерам. Поэтому поведение метода на некорректных данных описано в спецификации, хотя подобная ситуация в жизни редко встречается.

На самом деле, взглянув на любую из рассмотренных функций, в общем случае выделяют 4 основных класса эквивалентности (рис.5.3).

Это тот минимум, на котором и надо протестировать метод. Однако интуиция и опыт тестировщика подсказывают, что эти классы можно разбить на более мелкие подклассы, в которых часто возникают ошибки. Так, первый класс для функции нахождения частного мы разбили на 14 подклассов, в результате чего и обнаружили ошибку.

Помимо рассмотренных классов тестовых примеров, направленных на выявление различных дефектов в работе программной системы, выделяют также тестовые примеры реинициализации системы, повторного ввода данных, устойчивости системы и другие.

Источник

Накидать классы эквивалентности кэ на поле ввода номера дома

Что пишут в блогах

В этом видео я показал как можно визуализировать покрытие автоматическими тестами для GraphQL api с помощью инструмента Reqover.

Cегодня хочу поговорить с вами на тему комьюнити для тестировщиков.

Как и в любой сфере, среди тестировщиков существует куча различных комьюнити. Раньше они организовывались в скайпе.

Забываю похвастаться статусом книги.

Онлайн-тренинги

Конференции

Heisenbug 2021 Moscow
Большая техническая конференция для тестировщиков
5-7 октября 2021, онлайн

Что пишут в блогах (EN)

Разделы портала

Про инструменты

Ещё в самом начале предыдущего онлайн-тренинга «Практикум по тест-дизайну» я обещал ученикам написать о том, как выполнять разбиение входных данных на подобласти (классы эквивалетности) в ситуациях, когда в поле ввода можно указать произвольную строку, а по смыслу туда должно быть введено число. Увы, им пришлось выполнять домашние задания без моих подсказок (впрочем, может быть это совсем не плохо). Но я всё таки решил перед тем, как начнутся занятия следующей группы, написать небольшую “шпаргалку”.

Подавляющее большинство книг и статей, где описывается эта техника, в качестве примера рассматривают разбиение на классы множества чисел. При этом совершенно не учитывается тот факт, что в реальных приложениях с пользовательским интерфейсом все поля ввода строковые, и даже если есть ограничения на вводимые символы – это тоже предмет тестирования.

А что рекомендуется делать с “нечислами”? Они все объединяются в один большой класс “невалидных” данных, из него наугад берётся одно-два значения и всё.

Представление о том, что из себя представляет “число” сильно зависит от конкретной реализации, и я покажу вам распространённые примеры строк, которые с точки зрения программы являются числом, хотя не всякий об этом догадается. А также опишу общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности для строковых полей ввода, предназначенных для ввода числовых значений.

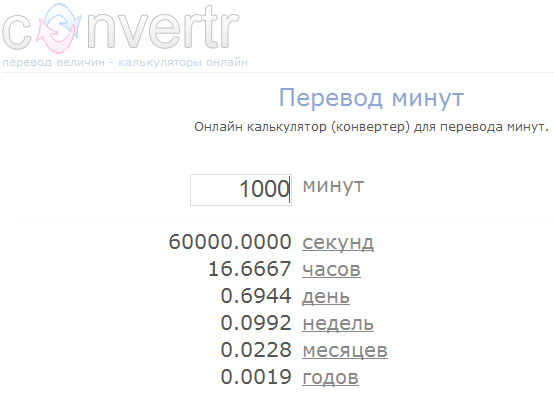
Итак, давайте представим себе, что у нас есть приложение, которое на вход принимает строку, но по смыслу она должна интерпретироваться как число. Например, вот такое: Онлайн-калькулятор для перевода единиц времени.

Все возможные строки, разумеется, можно разделить на два больших класса – “числа” и “нечисла”. Но я дам этим классам другие, более длинные, но при этом более точные названия:

В такой формулировке сразу становится ясно, что программа на вход получает строку, которая перво-наперво по каким-то правилам преобразуется в число. Если это преобразование прошло успешно – полученное число используется в вычислениях, результат которых мы можем наблюдать. А если преобразовать строку в число не удалось – мы получаем информацию об этом либо в виде сообщения о возникшей проблеме, либо в виде “бессмысленного” результата вычислений.

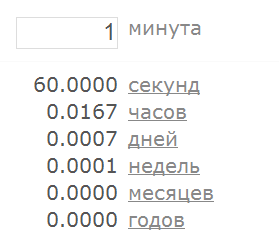
Мы можем без труда определить, как именно наш преобразователь времени ведёт себя в той и в другой ситуации, для этого достаточно подать на вход какое-нибудь значение, которое вне всяких сомнений должно интерпретироваться как число (например, “1”):

а также какое-нибудь значение, которое абсолютно точно числом не является (например, “привет”):

То есть здесь мы как раз имеем случай, когда “невалидное” входное значение приводить к бессмысленному результату (NaN означает “Not a Number”).

Теперь давайте попробуем определить, какие же строки программа будет интерпретировать как числа, то есть начнём выделять в наших больших классах подклассы меньшего размера, но зато описанные конструктивно. Начнём с простого:

1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число.

Очевидно? Вполне. Хотя нет, не совсем очевидно. Наверняка вы уже готовы были поймать меня за руку – какой длины последовательность цифр интерпретируется как число? Всё верно, правильный вопрос.

Чтобы ответить на него, нужно опять применить технику разбиения на подобласти. Впрочем, здесь мы как раз имеем достаточно простой случай – длина последовательности это целое неотрицательное число, так что техника работает в полном соответствии с учебниками.

Минимальная длина последовательности – ноль. Максимальная длина – “сколько влезет”.

А сколько влезет? И куда влезет? В обсуждаемом приложении не указано никаких ограничений на размер поля ввода. Может быть браузер накладывает какое-нибудь ограничение, но лично мне про это ничего не известно, и даже если оно есть – наверняка в разных браузерах оно разное. Если введённые данные передаются на сервер в виде GET-запроса, возможно, имеется ограничение на длину запроса – согласно стандарту RFC 2068 они должны поддерживать не менее 255 байтов, но конечно же все реально способны обрабатывать запросы большей длины, и конечно же это опять зависит от браузера и от веб-сервера.

Конвертер, который мы используем в качестве примера, реализован на языке JavaScript, на сервер никаких данных не отправляется, все вычисления производятся внутри браузера. Установленный на моём ноутбуке Google Chrome успешно справился со строкой, состоящей из 10 000 000 девяток, а вот строку из 100 000 000 девяток он обработать уже не смог – после длительного раздумья он вывел сообщение “Опаньки…” и предложил перегрузить страницу, потому что на ней возникла ошибка. Следовательно, где-то между этими значениями и находится та самая максимальная длина, определяемая по принципу “сколько влезет”. Поэтому уточняем:

1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число, если длина строки не превышает некоторое Максимальное Значение.

Впрочем, куда раньше, на существенно более коротких последовательностях, начинает наблюдаться вот такая картина (скриншот показывает ситуацию, когда введена последовательность из 1000 девяток):

При вычислениях возникло переполнение, однако Infinity – это не NaN, то есть согласно описанном выше уговору мы будем считать, что такая последовательность (а также и более длинные последовательности цифр) всё таки может считаться числом.

А что там с другой стороны? Последовательность нулевой длины – это пустая строка. Число ли это? Чуства и логика подсказывают, что нет, однако приложение не согласно с ними и интерпретирует пустую строку как число ноль:

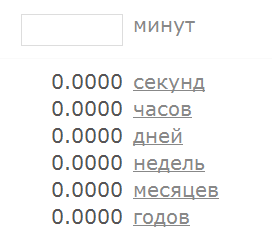
На всякий случай ещё проверим последовательности длины 1, как ближайшей к минимальной граничной.

Только чур не пытайтесь найти такую длину, при которой ещё не происходит переполнения, потому что это уже к длине не имеет никакого отношения, здесь важна уже не длина последовательности цифр, а само значение числа. Это оставим читателю в качестве упражнения (подсказка: JavaScript реализует стандарт IEEE-754 и может работать с числами двойной точности), а сами вернёмся к рассмотрению разных других строк.

С последовательностями цифр мы разобрались. Давайте попробуем добавить какие-нибудь “нецифры”. Перестанет ли строка быть числом?

Наверняка вы сами без труда вспомните некоторые случаи, когда этого (может быть) не случится – пробелы в начале и в конце, а также ведущие нули. Действительно, они обрезаются, а оставщаяся строка интерпретируется как число. Итак:

1.2 строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале некоторое количество нулей, при этом ведущие нули игнорируются,

1.3. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале или в конце некоторое количество пробелов, при этом все пробелы игнорируются.

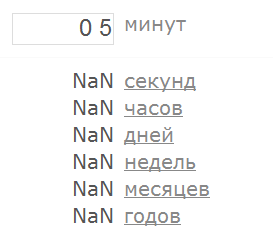
Ладно, двигаемся дальше – вспоминаем про отрицательные числа:

1.4. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начало знак минус или плюс.

Надеюсь про плюс никто не забыл, да? Кстати, между минусом/плюсом и первой цифрой могут быть пробелы. Ну и перед ними тоже, конечно.

Гм… Кажется, у нас проблема. Помните ещё про пустую строку? Мы же согласились считать её как бы числом. Зря согласились – если “перед ней” поставить минус или плюс, числа не получается.

Ладно, выкидываем пустую строку, будем рассматривать её отдельно, как особый случай, а минимальную длину последовательности цифр объявим равной единице.

Кстати, вас не насторожил тот факт, что я перестал говорить “целое число”? В правиле выделения подобласти 1.1 я его написал, а в следующих правилах нет.

Всё верно, эти правила работают также и для нецелых чисел. Добавляем новое правило:

1.5. строка, состоящая из двух неразрывных цепочек цифр, разделённых десятичной точкой, интерпретируется как число

Углубляться в подробности, связанные с точностью вычислений не станем, отметим лишь, что здесь тоже можно применить технику разбиения на подобласти. К чему применить? К количеству значащих цифр, или к количеству знаков после запятой, в зависимости от того, как интерпретируется понятие точности в конкретном приложении. Но при этом следует отметить, что для чисел с плавающей точкой техника разбиения на подобласти работает плохо, за подробностями я отправляю вас к статьям Виктора Кулямина про тестирование математических функций (нетерпеливые могут сразу заглянуть в конец раздела 4.3, а любопытные могут поискать ещё другие статьи и презентации на ту же тему на личной страничке Виктора).

А всё почему? Потому что JavaScript реализует стандарт IEEE-754.

Вообще-то к этому моменту вы, наверное, догадались, что я неспроста уже второй раз упомянул этот стандарт. Да, вы правы. Пришло время перейти к более сложным строкам, которые ну совсем не последовательности цифр, но при этом всё равно интерпретируются как числа. Давайте введём в наше приложение, например, число 120:

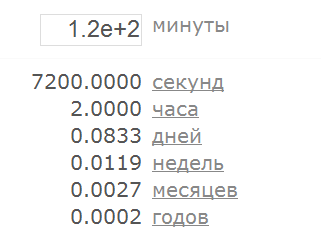
Оно работает! Думаете, это только этот конвертер такой, что я специально его выбрал? Ничего подобного! Откройте с десяток наугад выбранных веб-магазинов или онлайн-калькуляторов – добрая половина согласится принять числа в таком формате. А теперь сходите и проверьте своё собственное приложение.

Хотя нет, подождите. Это ещё не всё.

Во-первых, надо добавить ещё одно правило:

1.6. строка, состоящая из числа, за которым следует символ ‘e’, за которым следует целое число, интерпретируется как число

Да, 100e-1 = 10, а плюс можно не указывать, так что 1.0e2 = 1.0e+2 = 100.

А во-вторых, есть ещё и другие строки, которые тоже интерпретируются как числа, вот пример:

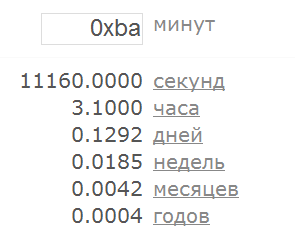
Все числа до этого момента у нас были в десятеричном представлении, а теперь появились шестнадцатеричные. Я намеренно в самом начале, когда ещё первый раз сформулировал правило 1.1 не стал акцентировать внимание на том, что такое “цифра”.

Что же, добавляем новое правило:

1.7. строка, состоящая из символов ‘0x’, за которыми следует неразрывная последовательность шестнадцатеричных цифр, интерпретируется как шестнадцатеричное целое число

Правило 1.1 при этом придётся тоже уточнить, указав, что там могут участвовать только десятеричные цифры. Приятной новостью является то, что шестнадцатеричные числа могут быть только целые (ну, то есть, в этом приложении так, может быть где-то и дробные бывают). Так что максимум, что можно ещё сделать с ними – добавить плюс/минус, да пробелы в начале и в конце.

Ну вот, теперь можете проверять своё приложение, сразу и на числа с плавающей точкой, и на шестнадцатеричные числа. А я тем временем расскажу ещё кое-что про строки, которые могут быть числами.

Однажды мне встретился интернет-магазин, который принимал не только числа в шестнадцатеричном представлении, но и в восьмеричном. То есть ноль в начале не игнорировался, как это бывает обычно, а свидетельствовал о том, что число следует интерпретировать как восьмеричное. Так что правило 1.2 тоже не надо вешать на стенку, и оно не всегда справедливо.

Попробуйте в наш подопытный конвертер ввести строку Infinity – вы удивитесь, но это тоже число (а в некоторых языках программирования распознаётся также строка Inf):

В качестве записной книжки для ведения списка дел я использую замечательный сервис Toodledo. Так вот, там при создании записи можно в поле ввода даты написать, например, “tomorrow” или “next Monday” – и оно работает! Для таких преобразований бывают даже специальные библиотеки, например, в языке Perl для анализа дат используется Date::Manip, а для анализа чисел Lingua::EN::Words2Num. Мне лично не приходилось тестировать приложения, где можно было бы вводить числа в текстовом виде, но такое действительно иногда встречается на практике.

Ещё одно любопытное “число”, специально для тех, кто знаком с языком программирования Perl – “0 but true”.

А вот пример приложения – калькулятор доходности вкладов, в котором число в шестнадцатеричном представлении проходит валидацию, которая выполняется средствами JavaScript, но вызывает проблемы при вычислениях на серверной стороне. Попробуйте указать сумму вклада в шестнадцатеричном виде, например, 0xff – и вы увидите, что серая табличка с расчётами не появится на странице. Добиться аналогичного эффекта, вводя положительные десятеричные числа, мне не удалось.

(Примечание: так работал калькулятор во время написания статьи, сейчас реализация уже изменилась)

Этот приём позволяет иногда “протолкнуть” через валидатор неправильное значение, которое может привести к сбоям на серверной стороне.

В общем, надеюсь, вы поняли, что “строка, которая может быть проинтерпретирована как число” – это не такая простая штука, как может показаться на первый взгляд.

А что же попадает во второй большой класс, “нечисла”. Туда попадает всё остальное.

Да, вот такое неконструктивное определение. И при этом я обещал в самом начале статьи рассказать вам общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности. Пожалуйста, вот эта схема, в одном абзаце:

Сначала считаем, что все строки находятся в классе “нечисел”. Как только вы прочитали в требованиях, или в документации, или узнали от коллег, или прочитали в какой-нибудь статье (например, в этой) о том, что строки определённого вида могут интерпретироваться как число – вы выделяете соответствующее подмножество строк и проверяете. Если оказалось, что ваше приложение не считает строки такого вида числами, вы сбрасываете всё обратно в большой класс “нечисел”. Ну а если приложение всё-таки согласилось считать эти строки числами, тогда они выделяются в отдельный подкласс и переводятся в класс “чисел”.

Вот и всё, очень простой алгоритм 🙂

Ну так что, принимает ваше приложение шестнадцатеричные числа или нет, а?

Источник

Adblock
detector

Определим алгоритм использования техники классов эквивалентности:

1. Определить классы эквивалентности.

2. Выбрать по одному тесту для каждого класса, выписать все тесты для всех классов.

3. Выполнить тесты.

Пример использования классов эквивалентности по алгоритму

на примере формы обратной связи сайта radar4site.ru:

На странице «Обратная связь» есть всего два элемента: поле для ввода сообщения и кнопка «Отправить».

1. Определим классы эквивалентности для поля ввода сообщения:

Попробуем выделить классы эквивалентности по двум направлениям: 

• По количеству символов.
• По типу символов (буквы, цифры, специальные символы).

1.1. По количеству символов:

1.1.1. Начнём вводить текст в поле ввода до тех пор, пока не появится ограничение на длину. В нашем случае интерфейс подсказал нам, что больше 1000 символов ввести не сможем в это поле. На всякий случай определим количество символов при помощи инструмента Количество символов.

1.1.2. Таким образом, найдено ограничение для длину поля — 1000 символов, т.е. это верхняя граница.

1.1.3. Какой будет нижняя граница? Меньше нуля ввести не сможем. А можно ли ввести 0 символов? Можно оставить поле пустым и нажать «Отправить», в таком случае считаем, что 0 символов допустимы. Поэтому нижняя граница — 0 символов.

1.1.4. Таким образом, определен класс эквивалентности «по количеству символов» с допустимой нижней границей 0 символов и допустимой верхней границей 1000 символов.

1.2. По типу символов:

1.2.1. Поскольку это поле для ввода сообщения, мы можем вводить любые символы, поэтому можно в одном классе проверять сразу множество символов разного типа (буквы, цифры, спец. символы).

1.2.2. Таким образом, определен класс эквивалентности «по типу символов».

2. Выбираем по одному тесту в каждом классе эквивалентности:

2.1. По количеству символов: любой текст длиной в 101 символов, например «Здравствуйте. Ваш сайт помог мне чуть лучше понять, чем занимаются тестировщики. Спасибо Вам большое!».

2.2. По типу символов: текст, содержащий символы разного типа, например: «йцукенгшщзхъфывапролджэячсмитьбю.,1234567890-=ё!»№;%:?*()_+@#$^&|/}{[]><«.

3. Выполним тесты (введя наши значения в поле ввода и нажав на кнопку «Отправить»). В нашем случае уже проверил — значения обработались успешно, ошибок нет, сообщение отправилось.

Теперь представим, сколько мы сэкономили времени. Для первого класса эквивалентности у нас вместо тысячи тестов всего один. Для второго класса эквивалентности мы сразу определили класс допустимых значений и не пришлось генерировать множество тестов, вместо этого у нас получится всего один тест.

Как ещё можно докрутить технику? Мы можем определить ещё несколько классов эквивалентности, например, проверить символы английского алфавита (других алфавитов), проверить другие специальные символы, проверить эмодзи, смайлики и т.д.

Похожие заметки:

Классы эквивалентности определение

Классы эквивалентности в тестировании

Автор: Алексей Баранцев

Ещё в самом начале предыдущего онлайн-тренинга «Практикум по тест-дизайну» я обещал ученикам написать о том, как выполнять разбиение входных данных на подобласти (классы эквивалетности) в ситуациях, когда в поле ввода можно указать произвольную строку, а по смыслу туда должно быть введено число. Увы, им пришлось выполнять домашние задания без моих подсказок (впрочем, может быть это совсем не плохо). Но я всё таки решил перед тем, как начнутся занятия следующей группы, написать небольшую “шпаргалку”.

Подавляющее большинство книг и статей, где описывается эта техника, в качестве примера рассматривают разбиение на классы множества чисел. При этом совершенно не учитывается тот факт, что в реальных приложениях с пользовательским интерфейсом все поля ввода строковые, и даже если есть ограничения на вводимые символы – это тоже предмет тестирования.

А что рекомендуется делать с “нечислами”? Они все объединяются в один большой класс “невалидных” данных, из него наугад берётся одно-два значения и всё.

И всё? А вот и нет!

Представление о том, что из себя представляет “число” сильно зависит от конкретной реализации, и я покажу вам распространённые примеры строк, которые с точки зрения программы являются числом, хотя не всякий об этом догадается. А также опишу общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности для строковых полей ввода, предназначенных для ввода числовых значений.

Итак, давайте представим себе, что у нас есть приложение, которое на вход принимает строку, но по смыслу она должна интерпретироваться как число. Например, вот такое: Онлайн-калькулятор для перевода единиц времени.

Все возможные строки, разумеется, можно разделить на два больших класса – “числа” и “нечисла”. Но я дам этим классам другие, более длинные, но при этом более точные названия:

1. множество строк, которые программа интерпретирует как числа;
2. множество строк, которые программа не может интерпретировать как числа.

В такой формулировке сразу становится ясно, что программа на вход получает строку, которая перво-наперво по каким-то правилам преобразуется в число. Если это преобразование прошло успешно – полученное число используется в вычислениях, результат которых мы можем наблюдать. А если преобразовать строку в число не удалось – мы получаем информацию об этом либо в виде сообщения о возникшей проблеме, либо в виде “бессмысленного” результата вычислений.

Мы можем без труда определить, как именно наш преобразователь времени ведёт себя в той и в другой ситуации, для этого достаточно подать на вход какое-нибудь значение, которое вне всяких сомнений должно интерпретироваться как число (например, “1”):

а также какое-нибудь значение, которое абсолютно точно числом не является (например, “привет”):

То есть здесь мы как раз имеем случай, когда “невалидное” входное значение приводить к бессмысленному результату (NaN означает “Not a Number”).

Теперь давайте попробуем определить, какие же строки программа будет интерпретировать как числа, то есть начнём выделять в наших больших классах подклассы меньшего размера, но зато описанные конструктивно. Начнём с простого:

1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число.

Очевидно? Вполне. Хотя нет, не совсем очевидно. Наверняка вы уже готовы были поймать меня за руку – какой длины последовательность цифр интерпретируется как число? Всё верно, правильный вопрос.

Чтобы ответить на него, нужно опять применить технику разбиения на подобласти. Впрочем, здесь мы как раз имеем достаточно простой случай – длина последовательности это целое неотрицательное число, так что техника работает в полном соответствии с учебниками.

Минимальная длина последовательности – ноль. Максимальная длина – “сколько влезет”.

А сколько влезет? И куда влезет? В обсуждаемом приложении не указано никаких ограничений на размер поля ввода. Может быть браузер накладывает какое-нибудь ограничение, но лично мне про это ничего не известно, и даже если оно есть – наверняка в разных браузерах оно разное. Если введённые данные передаются на сервер в виде GET-запроса, возможно, имеется ограничение на длину запроса – согласно стандарту RFC 2068 они должны поддерживать не менее 255 байтов, но конечно же все реально способны обрабатывать запросы большей длины, и конечно же это опять зависит от браузера и от веб-сервера.

Конвертер, который мы используем в качестве примера, реализован на языке JavaScript, на сервер никаких данных не отправляется, все вычисления производятся внутри браузера. Установленный на моём ноутбуке Google Chrome успешно справился со строкой, состоящей из 10 000 000 девяток, а вот строку из 100 000 000 девяток он обработать уже не смог – после длительного раздумья он вывел сообщение “Опаньки…” и предложил перегрузить страницу, потому что на ней возникла ошибка. Следовательно, где-то между этими значениями и находится та самая максимальная длина, определяемая по принципу “сколько влезет”. Поэтому уточняем:

1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число, если длина строки не превышает некоторое Максимальное Значение.

Впрочем, куда раньше, на существенно более коротких последовательностях, начинает наблюдаться вот такая картина (скриншот показывает ситуацию, когда введена последовательность из 1000 девяток):

При вычислениях возникло переполнение, однако Infinity – это не NaN, то есть согласно описанном выше уговору мы будем считать, что такая последовательность (а также и более длинные последовательности цифр) всё таки может считаться числом.

А что там с другой стороны? Последовательность нулевой длины – это пустая строка. Число ли это? Чуства и логика подсказывают, что нет, однако приложение не согласно с ними и интерпретирует пустую строку как число ноль:

На всякий случай ещё проверим последовательности длины 1, как ближайшей к минимальной граничной.

Только чур не пытайтесь найти такую длину, при которой ещё не происходит переполнения, потому что это уже к длине не имеет никакого отношения, здесь важна уже не длина последовательности цифр, а само значение числа. Это оставим читателю в качестве упражнения (подсказка: JavaScript реализует стандарт IEEE-754 и может работать с числами двойной точности), а сами вернёмся к рассмотрению разных других строк.

С последовательностями цифр мы разобрались. Давайте попробуем добавить какие-нибудь “нецифры”. Перестанет ли строка быть числом?

Наверняка вы сами без труда вспомните некоторые случаи, когда этого (может быть) не случится – пробелы в начале и в конце, а также ведущие нули. Действительно, они обрезаются, а оставщаяся строка интерпретируется как число. Итак:

1.2 строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале некоторое количество нулей, при этом ведущие нули игнорируются,

1.3. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале или в конце некоторое количество пробелов, при этом все пробелы игнорируются.

Всё верно? Нет! Во-первых, не забывайте про Максимальное Значение длины, если добавить слишком много нулей или пробелов, строка перестанет быть числом, даже если эти пробелы добавлялись к совершенно безобидному небольшому числу. Во-вторых, добавлять пробелы и нули можно только в строго определённом порядке — пробелы с краю, нули ближе к «основной части» числа, в другом порядке они уже не будут игнорироваться:

Да, можно эти правила уточнить, ввести понятие “неразрывной последовательности цифр”, к которой уже можно прибавлять пробелы. Но если вы собрались сейчас записать эти правила и повесить на стенку – не делайте этого! Вот вам пример приложения которое действует в точности наоборот – там можно вставлять пробелы куда угодно, хоть в начало, хоть в конец, хоть в середину. А есть и такие (в основном десктопные), в которых пробелы никуда нельзя вставлять, например, так ведёт себя диалог задания размера рисунка в графическом редакторе Paint в Windows 7.

Ладно, двигаемся дальше – вспоминаем про отрицательные числа:

1.4. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начало знак минус или плюс.

Надеюсь про плюс никто не забыл, да? Кстати, между минусом/плюсом и первой цифрой могут быть пробелы. Ну и перед ними тоже, конечно.

Гм… Кажется, у нас проблема. Помните ещё про пустую строку? Мы же согласились считать её как бы числом. Зря согласились – если “перед ней” поставить минус или плюс, числа не получается.

Ладно, выкидываем пустую строку, будем рассматривать её отдельно, как особый случай, а минимальную длину последовательности цифр объявим равной единице.

Кстати, вас не насторожил тот факт, что я перестал говорить “целое число”? В правиле выделения подобласти 1.1 я его написал, а в следующих правилах нет.

Всё верно, эти правила работают также и для нецелых чисел. Добавляем новое правило:

1.5. строка, состоящая из двух неразрывных цепочек цифр, разделённых десятичной точкой, интерпретируется как число

Углубляться в подробности, связанные с точностью вычислений не станем, отметим лишь, что здесь тоже можно применить технику разбиения на подобласти. К чему применить? К количеству значащих цифр, или к количеству знаков после запятой, в зависимости от того, как интерпретируется понятие точности в конкретном приложении. Но при этом следует отметить, что для чисел с плавающей точкой техника разбиения на подобласти работает плохо, за подробностями я отправляю вас к статьям Виктора Кулямина про тестирование математических функций (нетерпеливые могут сразу заглянуть в конец раздела 4.3, а любопытные могут поискать ещё другие статьи и презентации на ту же тему на личной страничке Виктора).

А всё почему? Потому что JavaScript реализует стандарт IEEE-754.

Вообще-то к этому моменту вы, наверное, догадались, что я неспроста уже второй раз упомянул этот стандарт. Да, вы правы. Пришло время перейти к более сложным строкам, которые ну совсем не последовательности цифр, но при этом всё равно интерпретируются как числа. Давайте введём в наше приложение, например, число 120:

Оно работает! Думаете, это только этот конвертер такой, что я специально его выбрал? Ничего подобного! Откройте с десяток наугад выбранных веб-магазинов или онлайн-калькуляторов – добрая половина согласится принять числа в таком формате. А теперь сходите и проверьте своё собственное приложение.

Хотя нет, подождите. Это ещё не всё.

Во-первых, надо добавить ещё одно правило:

1.6. строка, состоящая из числа, за которым следует символ ‘e’, за которым следует целое число, интерпретируется как число

Да, 100e-1 = 10, а плюс можно не указывать, так что 1.0e2 = 1.0e+2 = 100.

А во-вторых, есть ещё и другие строки, которые тоже интерпретируются как числа, вот пример:

Все числа до этого момента у нас были в десятеричном представлении, а теперь появились шестнадцатеричные. Я намеренно в самом начале, когда ещё первый раз сформулировал правило 1.1 не стал акцентировать внимание на том, что такое “цифра”.

Что же, добавляем новое правило:

1.7. строка, состоящая из символов ‘0x’, за которыми следует неразрывная последовательность шестнадцатеричных цифр, интерпретируется как шестнадцатеричное целое число

Правило 1.1 при этом придётся тоже уточнить, указав, что там могут участвовать только десятеричные цифры. Приятной новостью является то, что шестнадцатеричные числа могут быть только целые (ну, то есть, в этом приложении так, может быть где-то и дробные бывают). Так что максимум, что можно ещё сделать с ними – добавить плюс/минус, да пробелы в начале и в конце.

Ну вот, теперь можете проверять своё приложение, сразу и на числа с плавающей точкой, и на шестнадцатеричные числа. А я тем временем расскажу ещё кое-что про строки, которые могут быть числами.

Если ваше приложение написано на языке Pascal или Delphi, думаю, вам будет полезно знать, что в этом языке представляются в несколько ином виде – впереди стоит знак $ (доллар), а не 0x.

Однажды мне встретился интернет-магазин, который принимал не только числа в шестнадцатеричном представлении, но и в восьмеричном. То есть ноль в начале не игнорировался, как это бывает обычно, а свидетельствовал о том, что число следует интерпретировать как восьмеричное. Так что правило 1.2 тоже не надо вешать на стенку, и оно не всегда справедливо.

Попробуйте в наш подопытный конвертер ввести строку Infinity – вы удивитесь, но это тоже число (а в некоторых языках программирования распознаётся также строка Inf):

В качестве записной книжки для ведения списка дел я использую замечательный сервис Toodledo. Так вот, там при создании записи можно в поле ввода даты написать, например, “tomorrow” или “next Monday” – и оно работает! Для таких преобразований бывают даже специальные библиотеки, например, в языке Perl для анализа дат используется Date::Manip, а для анализа чисел Lingua::EN::Words2Num. Мне лично не приходилось тестировать приложения, где можно было бы вводить числа в текстовом виде, но такое действительно иногда встречается на практике.

Ещё одно любопытное “число”, специально для тех, кто знаком с языком программирования Perl – “0 but true”.

А вот пример приложения – калькулятор доходности вкладов, в котором число в шестнадцатеричном представлении проходит валидацию, которая выполняется средствами JavaScript, но вызывает проблемы при вычислениях на серверной стороне. Попробуйте указать сумму вклада в шестнадцатеричном виде, например, 0xff – и вы увидите, что серая табличка с расчётами не появится на странице. Добиться аналогичного эффекта, вводя положительные десятеричные числа, мне не удалось.

(Примечание: так работал калькулятор во время написания статьи, сейчас реализация уже изменилась)

Этот приём позволяет иногда “протолкнуть” через валидатор неправильное значение, которое может привести к сбоям на серверной стороне.

В общем, надеюсь, вы поняли, что “строка, которая может быть проинтерпретирована как число” – это не такая простая штука, как может показаться на первый взгляд.

А что же попадает во второй большой класс, “нечисла”. Туда попадает всё остальное.

Да, вот такое неконструктивное определение. И при этом я обещал в самом начале статьи рассказать вам общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности. Пожалуйста, вот эта схема, в одном абзаце:

Сначала считаем, что все строки находятся в классе “нечисел”. Как только вы прочитали в требованиях, или в документации, или узнали от коллег, или прочитали в какой-нибудь статье (например, в этой) о том, что строки определённого вида могут интерпретироваться как число – вы выделяете соответствующее подмножество строк и проверяете. Если оказалось, что ваше приложение не считает строки такого вида числами, вы сбрасываете всё обратно в большой класс “нечисел”. Ну а если приложение всё-таки согласилось считать эти строки числами, тогда они выделяются в отдельный подкласс и переводятся в класс “чисел”.

Вот и всё, очень простой алгоритм

Ну так что, принимает ваше приложение шестнадцатеричные числа или нет, а?

Обсудить в форуме

Содержание

• Что это
• Особенности
• Типы
• Советы
• Примеры
• Преимущества/недостатки
• Стандартные действия
• Чем отличается от анализа граничных значений

Коротко: выбранные тестировщиком наборы данных (диапазоны), которые подаются на ввод в модуль, и это должно приводить к одинаковым результатам.

Методика группировки и разделения тестовых входных данных на некие эквивалентные классы. Широко применяемая техника тестирования черного ящика; относится к базовым; всегда спрашивают на собеседованиях. Альтернативное название: эквивалентное разбиение.

Как гласит Первый принцип тестирования, “полное тестирование программы невозможно, или займет недопустимо длительное время”. Причина в том, что нужно проверить слишком много комбинаций тестовых данных. 

Например, слушатель курсов программирования написал простейший калькулятор, и нужно протестировать в нем (хотя бы) все возможные операции сложения (а их 10 в 16 степени, то есть 10 квадриллионов), на это понадобятся миллиарды лет.

Классы эквивалентности помогают тестировщику получить четкие результаты за ограниченное время, покрывая множество тестовых сценариев. Улучшается качество тест-кейсов, устраняется избыточность, возможная в других методиках.

Особенности

• Это методика черного ящика (то есть тестировщик не видит код, является “внешним наблюдателем” по отношению к программе)
• Еще одна формулировка КЭ: формируются группы (классы) тестовых вводов с одинаковым поведением
• Суть в том, что если один член класса ведет себя каким-то образом, то и все остальные члены должны вести себя так же
• Применяется на любом этапе жизненного цикла тестирования
• В том числе в юнит-тестировании, интеграционном, системном и приемочном тестировании
• Тест-кейсы основаны на классах (а не на отдельных тестовых вводах, которых может быть огромное количество). Это экономит рабочее время, потому как не создается много избыточных тест-кейсов.
• Техника применяется, когда тестовые данные можно поделить на интервалы и наборы дискретных значений (то есть почти всегда)
• Как правило, в QA применяется сочетание классов эквивалентности и граничных значений — это дает более надежные результаты.

Стандартные действия по методике

1. Правильно определяются классы эквивалентности, это главное.
2. Выбирается один представитель (член) в каждом классе. Из каждого эквивалентного набора тестов выбирается один тест.
3. Выполнение тестов от каждого класса.
4. Если времени достаточно (или ситуация требует, см. далее о типах), берутся несколько членов из каждого класса. Но у опытного тестировщика классы определены правильно с начала, поэтому несколько членов будут не обязательны (избыточны = покажут те же результаты).

Пример

Есть приложение, принимающее на ввод число из 2 или 3 цифр. Из условия понятно, что диапазон возможных чисел — достаточно большой, и все варианты проверить получается неэкономно. 

• Теперь эти числа группируем, формируя из них классы эквивалентности. Вместо проверки сотен чисел сформируем из них 4 эквивалентных класса, и разделим вводы на категорию валидных и невалидных.
• Один элемент из класса как бы представляет весь класс. Например, число 122 представляет класс “трехзначные числа”. Поданное на ввод, число 122 не вызывает ошибку в приложении (тест пройден). Из этого делаем вывод, что все другие члены класса “Трехзначные” также будут нормально приняты приложением. А если тест не пройдет с числом 122, то предполагается, что все трехзначные числа будут вызывать ошибку.
• А теперь берем число 7 из класса “однозначные числа”, то есть невалидный ввод. Ожидается, что приложение выдаст ошибку в ответ на заведомо невалидный ввод, и это будет значить, что оно работает правильно, и предполагается, что остальные однозначные числа также будут вызывать ошибку.

Еще пример

Есть приложение, в которое подается число от 10 до 100, и затем вычисляется его корень. Эквивалентные классы будут такими:

Класс	Описание
Числа от 10 до 100	Дата-сет для позитивного сценария
Числа от 0 до 9	Дата-сет для негативного сценария
Числа больше 100	Тоже не примет приложение
Отрицательные числа	Усложняем задачу
Буквы	Еще усложняем
Специальные символы типа %^&#	И еще такой отдельный класс

Типы классов эквивалентности ( * )

• Weak Normal. Тестируется по одной переменной из каждого класса. Поэтому еще называется предположением об одной ошибке (single fault assumption)
• Strong Normal, или предположение о нескольких ошибках. Создаются тест-кейсы из каждого элемента в множестве прямого произведения эквивалентности. Это улучшает охват тестирования, поскольку покрывает все возможные классы, позволяя проверить все возможные комбинации вводов.
• Weak Robust, как и Weak Normal, тестирует одну переменную из каждого КЭ, но фокусируется на тест-кейсах с невалидными значениями.
• Strong Robust. Создаются тест-кейсы для всех валидных и невалидных элементов произведения эквивалентного класса. Это “неэкономный” тип КЭ, не уменьшающий избыточность тест-кейсов.

Советы 

• Robust-типы применяются, если условия ошибки являются высокоприоритетными для проверки, и в сложных функциях
• Robust применяется, если невалидные значения вызывают runtime-ошибки в системе (в языках со строгой типизацией)
• Берутся одно валидное и оно невалидное значение, если входные условия в приложении не очень ясны
• Установление правильной эквивалентности может требовать опыта, и усилий
• Чем больше создано классов, тем вероятнее, что много тестов окажутся избыточными
• И чем меньше классов, тем выше вероятность пропуска ошибок

Преимущества и недостатки

Плюсы

• Главное — уменьшает количество тест-кейсов, не уменьшая покрытие
• Уменьшает время тестирования и упрощает процесс, меньше данных обрабатывается
• Применяется на всех этапах и уровнях тестирования
• Позволяет сфокусироваться на небольших наборах данных, что улучшает вероятность найти больше багов
• Тесты получаются более структурированными
• Подходит для проектов с ограничением времени и ресурсов (то есть всегда)

Минусы

• Не учитывает условия по граничным значениям (поэтому надо сочетать с анализом граничных значений)
• Подбор эквивалентных классов — сложная вещь для новичков

Разница между классами эквивалентности и анализом граничных значений

Классы эквивалентности	Граничные значения
Стандартная техника «черного ящика», с которой начинают тестирование	Часто последующий этап «черного ящика», продолжение тестирования после эквивалентных классов
Применяется на любом этапе тестирования: юнит-, интеграционное, системное, и пр.	Как дополнение к КЭ и как часть негативного или стресс-тестирования
Техника: тестовые данные делятся на эквивалентные классы, которые “должны вести себя одинаково”	Техника: проверяются “значения на границах” классов
Экономит время на тестирование, меньше тест-кейсов и они более эффективные	Уменьшает общее время выполнения тестов, делая поиск багов быстрее и проще
Стандартно тестируется только по одному значению из каждого эквивалентного класса	Тест-кейсы создаются из граничных значений классов
Альтернативное название: эквивалентное разбиение	Альтернативное название: проверка границ диапазона

В этой статье мы разберем одну из самых известных и фундаментальных техник, технику выделения классов эквивалентности и граничных значений.

В чем суть техники?

Основная задача определения классов эквивалентности и граничных значений — «уйти» от дублирующих проверок. Таким образом, мы сократим количество однотипных тестов до необходимого минимума. Как это можно представить?

Предположим, у нас много-много разных булок, сделаны они по одному рецепту, а вот форма у них немного разная. А теперь представьте, что вам необходимо определить вкус каждой булки. Что вы будете делать? Попробуете все или возьмете только одну, потому что остальные сделаны аналогично? Я думаю второй вариант будет более оптимальным)

В тестировании ситуация аналогичная. Только вместо булок наши тесты. И все немного сложнее.

Классы эквивалентности

Сначала дадим определение классам эквивалентности.

Эквивалентная область (equivalence partition) —часть области входных или выходных данных, для которой поведение компонента или системы, основываясь на спецификации, считается одинаковым.

Скорей всего было не очень понятно…

Проще говоря, любой тест, выполненный из одного и того же класса эквивалентности, приведет к точно такому же результату, как и выполнение всех остальные тестов из этого же класса.

Например, у нас есть 10 тестов из одного класса. Если один из этих тестов проходит корректно, и то все остальные пройдут корректно. И наоборот, если один из тестов приведет к падению системы, то и все остальные тесты, также приведут к падению.

Пока все еще абстрактно, давайте конкретизируем. Предположим, у нас планируется акция «Скидка 10% на покупку от 5 товаров». Нам необходимо проверить функционал скидки в зависимости от количества товаров. Что будем делать? Есть два варианта проверки:

1. Проверить, что скидки нет при покупке 1-го, 2-х, 3-х и 4-х товаров, начиная с 5 и так далее скидка в 10%. Т.е. на каждое число товаров проводить 1 тест.

Тестов получается очень много.

2. Попробовать выделить классы эквивалентности и оптимизировать проверки.

Пойдем по второму варианту, он более эффективный. У нас всего два разных результата выполнения теста — со скидкой и без скидки. Логично предположить, что класса эквивалентности тоже будет два. В одном тесты будут проверять наличие скидки в 10%, в другом ее отсутствие.

Графически это можно представить следующим образом:

Т.е. какой бы мы тест не взяли из первого класса, мы получим скидку в 0%, аналогично для второго класса эквивалентности.

Теперь теория и здравый смысл подсказывают нам, что можно взять не все тесты, а только несколько из каждого класса эквивалентности. Этого должно быть достаточно, чтобы проверить оба случая со скидкой.

Но теперь вопрос, какие тесты брать? Есть ли разница между ними, может быть все-таки есть небольшие отличия?

Граничные значения

Путем долгого времени наблюдения за разработкой и анализа багов, специалисты пришли к выводу, что большинство ошибок возникает именно на границах между классами эквивалентности. Т.е. нам в первую очередь важно проверить переходы на стыке границ каждого класса, так как именно там велик риск возникновения ошибок.

Поэтому для эффективного тестирования нам необходимо выделить у каждого класса граничные значения. Давайте попробуем сделать на нашем примере:

1. Скидка 0% действует при покупке от 1 до 4 товаров, следовательно будут два граничных значения: 1 и 4.
2. Скидка 10 % действует при покупке от 5 товаров и выше, т.е. граничное значения для второго будет — 5. По поводу второй границы класса необходимо смотреть в реализацию, она должна быть равна максимальному числу товаров, которое можно положить в корзину. Чтобы не усложнять себе работу, возьмем максимальное число товаров — 100.
3. Таким образом, мы с вами определили верхнюю и нижнюю границу каждого класса. Эти значения мы и возьмем в тестирование. Получаем таблицу:

Итого, 4 теста вместо 100 с учетом сохранения тестового покрытия.

Наша задача, как тестировщика, уметь правильно определить и работать с классами эквивалентности и граничными значениями. Выше мы рассмотрели пример с позиции черного ящика. У него есть существенные минус, мы не знаем как реализована работа функционала с точки зрения кода. Следовательно, не можем со 100% уверенностью правильно выделить классы эквивалентности.

Давайте рассмотрим пример посложней. Нам необходимо проверить корректность бокового меню на сайте из 10 страниц. Вот такое:

Страницы сами по себе одинаковые и отличаются только содержанием, боковое меню зрительно полностью идентично.

Только что пройденный материал подсказывает нам, что есть один класс эквивалентности и он включает в себя все 10 страниц. Но на практике есть как минимум два варианта:
1. Если сайт сделан на HTML, в том числе и боковое меню, то необходимо проверять КАЖДУЮ страницу, так как на каждой странице боковое меню работает отдельно от остальных.
2. Если сайт сделан с помощью, например, шаблонизаторов, то тогда выделить 10 страниц в класс эквивалентности можно, так как код меню хранится отдельно.

Т.е. в зависимости от реализации, классы будут разные. Как это определить? Если вы знаете языки программирования и у вас есть доступ в репозиторий, то посмотреть в код. Если вы не поняли, что я сейчас написал, то подойдет и второй вариант) Поговорите с программистом, который делал эту функциональность и уточните у него, правильно ли вы делаете.

Рассмотрим теперь некоторые специальные
бинарные отношения, используя введённые
обозначения и представления, а также
дадим некоторые новые определения.

Назовём отношение _A = {(x, x) | xA}диагональнымотношением множестваA. Это самый узкий
класс эквивалентностей, возможный в
некоторой системе обозначений. Обычно
это просто отношение равенства наА:_A = {(x, y) | xA & yA & x=y}.
Графически ему соответствует набор
вершин с петлями без рёбер между
вершинами. Матрица такого отношения
будет диагональной (единичной) логической
матрицей. Отсюда название.

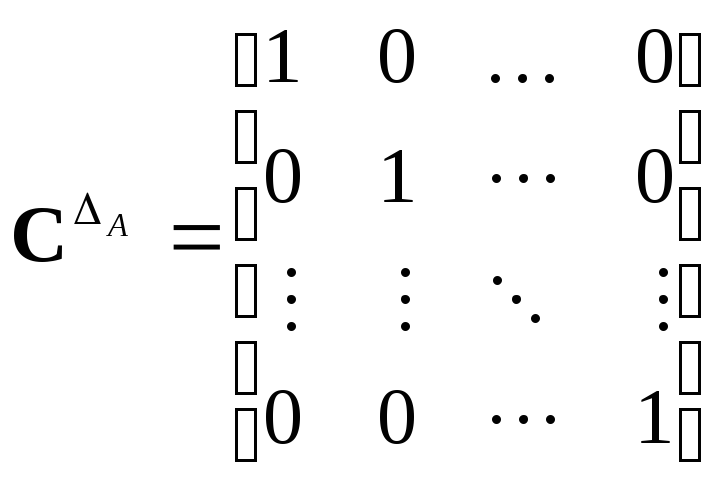
Рассматривавшееся свойство рефлексивности
может тогда быть выражено формулой
_A  .

Симметричность можно выразить формулой
^-1 =.

Транзитивность можно выразить формулой
.
(можно написать и²)

Таким образом, получаем определение
для отношения эквивалентности

 — эквивалентность на множестве A(_A  &^-1 =&).

Если - некоторое
бинарное отношение (AA),
аx– некоторый элемент
(xA),
то для этого элемента можно указать
множества элементов, связанных с ним
потак, что он будет
являться первым элементом в упорядоченной
паре {y | (x, y)}.
Графически это можно представить как
все вершины, куда можно попасть изxза один шаг:

Аналогично можно указать и множество
{y | (y, x)},
вершин, где начинаются стрелки, идущие
вx.

Но если ^-1 =то {y | (x, y)}={y | (y, x)}.
Для симметричных отношений обозначим
такое множество как

[x]_ = {y | (x, y)}
= {y | (y, x)}

Если это эквивалентность, то будем называть
[x]_классом эквивалентностиэлементаxпо отношению.
Это есть простомножество элементов,
эквивалентных x.
При этом элементxназываютобразующимкласса [x]_.

Для классов эквивалентности некоторого
AAследует отметить следующие свойства.

1. Каждый элемент принадлежит своему
   классу эквивалентности.

xA x[x]_

Это свойство следует из рефлексивности
:

_A  xA (x, x)
xA
x[x]_

1. Каждый элемент из класса образует в
   точности тот же самый класс.

y[x]_[y]_ = [x]_

Для обоснования необходимо использовать
и свойство симметричности, и свойство
транзитивности:

y[x]_(y, x)& (x, y)по определению [x]_и симметричности

Покажем что [y]_  [x]_,
то есть, чтоz[y]_z[x]_

z[y]_(z, y)& (y, z)по определению [y]_и симметричности.

Имеем (z, y)& (y, x)

По транзитивности и определению [x]_получаем (z, x)  z[x]_

Аналогично покажем [x]_  [y]_,
то есть, чтоz[x]_z[y]_

z[x]_(z, x)& (x, z)по определению [x]_и симметричности.

Имеем (z, x)& (x, y)

По транзитивности и определению [y]_получаем (z, y)  z[y]_

Из [y]_  [x]_и [x]_  [y]_получаем [y]_ = [x]_

Следующий возможный фрагмент графа
поясняет эти 4 связи (рефлексивность
непосредственно не используется для
доказательства, но петли на графе
приведены для иллюстративных целей, – это эквивалентность):

То есть, если zэквивалентенx, аxиyэквивалентны между
собой, тоzэквивалентен
каждому из них. Фактически, класс [z]_совпадет с [x]_и [y]_.

Рассмотренное свойство можно сформулировать
и в виде следующей фразы:

1. Каждый класс эквивалентности
   представляет собой в точности множество
   всех своих образующих элементов.

1. Два класса либо не имеют общих
   элементов, либо полностью совпадают.

Возможные формулировки:

xA yA ([x]_  [y]_ = )  ( [x]_ = [y]_ )

или

([x]_  [y]_ )([x]_ = [y]_)

([x]_  [y]_)([x]_  [y]_ = )

Таким образом, каждый класс эквивалентности
представляет собой полносвязнное по множество, а между разными классами
связейнет. Пример
фрагмента графа, удовлетворяющего этому
условию, показан на рисунке.

В множестве Aвыделено
два класса эквивалентности
[x]_=[y]_=[z]_={x, y, z}
и [u]_=[v]_={u, v}.
Эти классы образуют разбиение множестваA. Это множество
(множество классов) называется
фактормножеством. Для него используется
следующее обозначение:

= { [x]_ | xA }

В данном примере
= {{x, y, z}, {u, v}}

Вообще разбиением некоторого
множества A называют
семейство множеств (множество S
из множеств C),
таких, что они

1. не пустые

2. в объединении покрывают всё множество
   A

3. попарно либо не пересекаются, либо
   полностью совпадают

(CS C)
&
&
(C₁S
C₂S
((C₁C₂=)  (C₁=C₂)))

При этом сами множества из семейства
называют классами разбиений.

Покажем, что любое такое разбиение
порождает некоторое отношение
эквивалентности ,
которое можно охарактеризовать как
свойство «принадлежать одному классу
разбиения»:

 = {(x, y) | CS xC & yC}

Рефлексивность: xA
&
CS 
xC 
(x, x).

Симметричность: Следует из коммутативности
связки & в определении .

Транзитивность:

(x, y)
& (y, z)

(C₁S 
xC₁ & yC₁)
& (C₂S 
yC₂ & zC₂)


(C₁S
C₂S 
xC₁ & yC₁
& 
yC₂ & zC₂
&
C₁C₂
& C₁=C₂)


(CS xC & zC)(x, z)

Важным примером отношений эквивалентности
являются отношения, получаемые при
функциональном отображении одного
множества на другое. Допустим, f B^A.
Построим отношениеAAследующим образом:

 =  {(x, y) |  f(x)=f(y) }

Тогда оно будет являться отношением
эквивалентности. Эквивалентными будут
элементы, которым функция fставит в соответствие одинаковые
значения (в смысле некоторого отношения
равенства на множествеB).
При этом классом эквивалентности будут
множества всех тех элементов вA,
для которых значения функции равны:

[x]_ = {y | f(x)=f(y) }

Следующая диаграмма показывает пример
такого отношения:

То, что данное отношение действительно
является эквивалентностью, непосредственно
следует из аналогичных свойств отношения
= на множестве B.

Примеры отношений
эквивалентности: Сравнимость. Конгруэнция.

В теории чисел часто рассматривается
следующее отношение эквивалентности.
По некоторому натуральному числу nлюбоецелоечислоxможно единственным образом представить
в видеx=an+bтак, чтобы 0≤bиb<n.
Тогдаbназывают
остатком от деленияxнаn. При фиксированномnbможно рассматривать в качестве результата
вычисления некоторой функции:b=R_n(x).
Определяя по рассмотренной схеме для
этой функции отношение эквивалентности,
получаем отношение «иметь одинаковые
остатки от деления наn»:_n =  {(x, y) |  R_n(x)=R_n(y) }.
Такое отношение называетсясравнением
по модулюn. Для него
в математике используется специальное
обозначение

xy (modn)

Читается: «xсравнимо
сyпо модулюn».

Каждый класс эквивалентности для этого
отношения представляет собой множество
чисел, дающих определённый остаток от
деления на n, и называетсяклассом вычетов по модулюn.
Обозначаются эти классы обычно просто
символами квадратных скобок вокруг
числа, выбранного образующим элементом
класса. Обычно числоnясно из контекста. Образующими обычно
берут минимальные неотрицательные
элементы классов.

Пример для n=3. Возможны
три вида остатков: 0, 1, 2. Множество всех
классов вычетов по модулю 3 будет
{[0], [1], [2]}. Число 7 и число 13 оба дают
остаток от деления на 3, равный 1. Поэтому
пишут 713 (mod 3),
при этом 7[1]
и 13[1].

Множество всех целых чисел обычно
обозначают символом ℤ,
а множество всех классов вычетов по
модулюnобозначаютℤ_n.
Например,
ℤ₃={[0], [1], [2]}.

Для операции сложения целых чисел +
такое разбиение на классы эквивалентности
обладает важным свойством:

ab (mod
n) &
cd (mod
n) 
a+cb+d (mod
n)

Получается, что данное отношение
эквивалентности «согласовано» с
некоторой операцией на разбиваемом
множестве.

Отношение эквивалентности, согласованное
с некоторой ассоциативной операцией
на разбиваемом им на классы множестве,
называется конгруэнцией:

(a, b)& (c, d) (a∗c, b∗d),

где ∗–
некоторая ассоциативная бинарная
операция.

Таким же свойством сравнение по модулю
nобладает и по отношению
к умножению целых чисел:ab (modn) &cd (modn)acbd (modn).

Конгруэнция – основной способ получения
конечных алгебр (особенно недвоичных)
из бесконечных. Она позволяет определять
операции между классами на основе
операций между образующими элементами.

Операцией между классами называют
множество возможных значений результатов
операции между элементами классов:

[x]_∗[y]_={ u∗v | u[x]_ & v[y]_ }

Для конгруэнции имеет место следующее
представление:

[x]_∗[y]_=
[x∗y]_

Для рассмотренного примера сравнения
по модулю 3 можно построить следующие
алгебры сложения и умножения классов:

+	[0]	[1]	[2]
[0]	[0]	[1]	[2]
[1]	[1]	[2]	[0]
[2]	[2]	[0]	[1]

	[0]	[1]	[2]
[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]
[2]	[0]	[2]	[1]

Такая алгебра классов с операциями + и
называется кольцом
классов вычетов по модулю 3. Например,
выражение [2]+[2]=[1] означает, что если
сложить любые два числа, дающие остаток
от деления на 3 равный 2, то получится
число, дающее остаток от деления на 3
равный 1.

Примеры отношений
эквивалентности: Эквивалентность
(равномощность) множеств. Мощность
множества. Счётные и несчётные множества.

Еще одним примером отношения
эквивалентности является уже упомянутая
эквивалентность (равномощность)
множеств: A~B(f B^A  ( f ^-1 A^B)). То, что это действительно отношение
эквивалентности, следует из следующего:

1. Рефлексивность. Каждое множество
   равномощно самому себе. Рассматривая
   отношение _Aкак функцию, ставящую каждому элементу
   множестваAего
   самого,_A
   A^A,xA _A(x)=x(эта функция биективная, так как
   (_A)^-1=_A)
   видим, чтоA~A.
   То, что некоторая функция устанавливает
   равномощность, удобно обозначать,
   надписывая её обозначение над символом
   ~:
   .

2. Симметричность.
   .

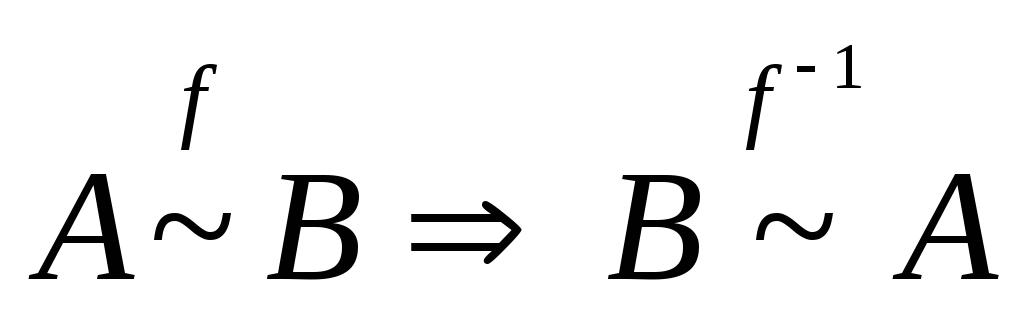3. Транзитивность.
   

Классы эквивалентности отношения ~
представляют собой множества из всех
множеств, равномощных некоторому
образующему элементу (множеству).
Обозначаются они обычно вертикальными
чертами с обеих сторон от выбранного
образующего элемента (множества) –
представителя класса:

|A| = { B |A~B }

Такой класс эквивалентности называют
мощностью множества. Для
конечных множеств представление о
таких классах можно считать отвлечённым
представлением о числе, возникающим
при рассматривании разнородных наборов
предметов, общим для которых является
именно количество предметов в наборах.
Для бесконечных множеств их мощности
представляют дальнейшее развитие
понятия числа.Мощности произвольных
множеств называют кардинальными
числами.Множества, равномощные
множеству натуральных чиселℕ,называют счётными множествами.В математике известны примеры построенных
определений для бесконечных множеств,
не являющихся счётными, например
множество всех функцийℬ^ℕ(ℬ={0, 1})
не является счётным. Это множество
можно представить как множество всехбесконечныхдвоичных последовательностей.
В каждой последовательности на позиции
с номеромjℕ
записано одно из двух возможных
значений 0 или 1 (как функция от номера
позиции). Если бы всё множество таких
последовательностей было счётным
(каждой последовательности был бы
назначен номерiℕ),
последовательности можно было бы
представить в видеa_ij,
гдеi– номер
последовательности,j– номер позиции. Но тогда можно построить
новую последовательность, не совпадающую
ни с одной из перечисленных по формуле

jℕ  b_j = a_jj

Эта последовательность, на каждой
позиции которой с номером jзаписано значениеb_j,
отличается от всех последовательностей,
которые можно данным образом занумеровать
(от каждой занумерованной последовательности
она отличается, по крайней мере, в
позиции, равной номеру последовательности).
С другой стороны, она также (как функция
от номера позиции) является элементом
множестваℬ^ℕ.
То есть, каково бы ни было отображение
изℕвℬ^ℕ,
вℬ^ℕостанутся незанумерованные элементы
(функции), что и показывает несчётностьℬ^ℕ.

Для конечных множеств само число
элементов выбирают в качестве обозначений
их мощности, пишут |A|=n,
имея в виду, что каждому натуральному
числуnℕвзаимнооднозначно сопоставлен некоторый
класс множеств, равномощныхK_n–
множеству натуральных чисел от 1 доn.
Мощность самого множестваℕтрадиционно обозначают |ℕ|=₀(древнееврейская буква алеф с индексом
0, обычно произносят «алеф-ноль»,
индексирование используется для
указания порядковых типов множеств,
здесь не рассматривается). Мощность
множестваℬ^ℕобозначают как |ℬ^ℕ|=(алеф без индекса) или готической буквойc,
и называютмощностью континуума.

Примеры отношений
эквивалентности: подобие (изоморфизм)
бинарных отношений (ориентированных
графов).

Следующий пример связан непосредственно
с самим предметом рассмотрения –
бинарными отношениями. Допустим, задано
два бинарных отношения, каждое на своем
множестве:   AAи  BBи имеется биективная функция со следующим
свойством:

fB^A & f ^-1A^B & (xA yA
( (x, y) ↔ (f(x), f(y)) ) )

Следующий рисунок иллюстрирует пример
такого отображения.

Везде, где есть связь по отношению вA, есть связь между
соответствующими отображениями по
функцииfвBпо. И наоборот,
если нет связи вAмежду некоторыми элементами, то нет и
связи между их отображениями вB.
Например, (a, b),f(a)=p,f(b)=qи (p, q).
Где есть петля в графе,
есть петля в графев вершине, соответствующей вершине с
петлей впо функцииf.

Отношения, между которыми можно
установить такие отображения, называются
подобными.

Возможность установить такое отображение
называется отношением подобия. Отношение
подобия обозначим инфиксным символом
.

    AA&  BB&

(
f  B^A  ( f ^-1  A^B
) & (xA yA
( (x, y) ↔ (f(x), f(y)) ) )

Как и с равномощностью множеств, для
удобства будем надписывать над символом обозначение функции, устанавливающей
данное соответствие.

Покажем, что подобие отношений является
отношением эквивалентности.

1. Рефлексивность.
   

2. Симметричность.
   

3. Транзитивность.
   

Классы эквивалентностей отношения
подобия представляют собой множество
всех отношений, имеющих определенную
структуру связей между элементами без
учета названий элементов и отношений.
С точки зрения рассмотрения графов
подобных отношений, подобие – это
свойство иметь одинаковую форму графа.
В рассмотренном примере оба графа могут
быть описаны словами «три вершины, одна
стрелка и петля в вершине, куда входит
стрелка». Такие классы эквивалентностей
можно назвать абстрактными отношениями.
Их можно изображать графами, не подписывая
узлов. Важно, что все свойства отношений,
рассматриваемые здесь, не зависят от
названий отношений, названий элементов
и интерпретации отношения в предметной
области. С другой стороны, изучив
свойства какого-либо конкретного
отношения, фактически мы изучили
свойствавсехотношений данного
класса. Для рассмотренного примера
граф абстрактного отношения выглядит
так:

Число различных классов отношений
вообще-то меньше, чем самих отношений.
Например, для двоичного множества все
отношения могут быть представлены
логическими матрицами 22.
Таких матриц 16. Некоторые из них будут
представлять подобные отношения.
Разбиение множества таких матриц на
классы эквивалентности по подобию
соответствующих им отношений представим
ориентированными графами и укажем
матрицы, реализующие эти отношения.
Видно, что число классов (форм конфигураций
связей) будет 10. Некоторые классы имеют
по две реализации.